PROBLEMA 2.5

Un generador de señales está conectado a una línea de transmisión cuya impedancia característica vale 100 Ω. La línea mide 10 metros y el dieléctrico en su interior tiene una permitividad relativa de 8.8. Al final de la línea se conecta una carga cuya impedancia de entrada vale 100 Ω. SI el generador tiene una resistencia interna de 1 Ω y un voltaje de salida en circuito abierto igual a 3cos(2π x 10⁸)t V, encuentre a)las expresiones matemáticas instantáneas para el voltaje y corriente en cualquier punto de la línea, y b)la potencia promedio que se le entrega a la carga.

SOLUCIÓN.

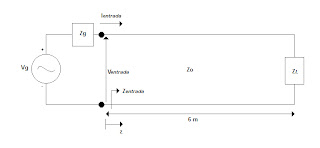
De acuerdo con los datos proporcionados, el circuito se puede representar de la siguiente forma:

Vg = 3 / 0                 f = 100 MHz

    Zg = 1 Ω               Zo = 100 Ω – ZL

Como la línea está acoplada, la impedancia que se ve en todos los puntos de la línea es la misma y, por lo tanto, la impedancia de entrada también vale eso:

                                                                     Zentrada = 100 Ω

La parte izquierda del circuito se puede representar ahora como:

De donde:

Ventr = [ Zentr / Zg + Zentr ] Vg = (100/101)(3/ 0) = 2.97 / 0 V

Ientr = (1 / Zg + Zentr)Vg =

 3 / 0 / 101 = 0.0297 / 0 A

Si se considera que la atenuación α es despreciable, entonces:

γ = jβ = jω /v = jω√εr / c = j(2πx10⁸)√8.8 /3x10⁸ = j6.2129 rad/m

Por lo tanto, se tiene que para cualquier punto de la línea a una distancia z a la derecha de las terminales de la entrada, el voltaje está dado por:

V(z) = (Ventr)exp(-jβz) = (2.97expj0)exp(-j6.2129) = 2.97exp(-j6.2129) V

Y acordemente la corriente es igual a:

I(z) =(Ientr)exp(-jβz) = 0.0297exp(-j6.2129) A

Finalmente, se obtinen las expresiones perdidas en función del tiempo, para cualquier punto de la línea:

V(z,t) = Re[V(z)exp(jωt)] = Re[2.97exp(-j6.2129) * exp(j2πft)]

V(z,t) = 2.97cos[2πx10⁸t – 6.2129] V

I(z,t) = Re[I(z)exp(jωt)] = Re[0.0297exp(-j6.2129) * exp(j2πft)]

I(z,t) = 0.0297cos[2πx10⁸t - 6.2129] A

Para el punto específico donde está la carga, las expresiones instantáneas se obtienen sustituyendo z = 10 m  en las ecuaciones anteriores.

Por lo que se refiere a la potencia promedio entregada a la carga, está debe ser igual a la potencia promedio de entrada, ya que está considerando que la línea no tiene pérdidas (α=0). De allí que, a partir de los fasores de volaje y corriente:

(Pprom) = (Pprom)entr = ½ Re(V(z)I’(z))

                 = ½ Re[2.97exp(-j6.2129)* 0.0297exp(j6.2129)]

                 = ½ (2.97 x 0.0297) = 0.0441045 W.