Plan de Estudios de la materia de Ondas Electromagnéticas Guiadas.

Aquí se encuentra el link del plan de estudios.
http://www.ice.esimez.ipn.mx/sites/www.ice.esimez.ipn.mx/files/programas2004/ondas_electromagneticas.pdf

FIbra Óptica.

La fibra óptica es un medio de transmisión empleado habitualmente en redes de datos; un hilo muy fino de material transparente, vidrio o materiales plásticos, por el que se envían pulsos de luz que representan los datos a transmitir. El haz de luz queda completamente confinado y se propaga por el interior de la fibra con un ángulo dereflexión por encima del ángulo límite de reflexión total, en función de la ley de Snell. La fuente de luz puede ser láser o un LED.

Las fibras se utilizan ampliamente en telecomunicaciones, ya que permiten enviar gran cantidad de datos a una gran distancia, con velocidades similares a las de radio o cable. Son el medio de transmisión por excelencia al ser inmune a las interferencias electromagnéticas, también se utilizan para redes locales, en donde se necesite aprovechar las ventajas de la fibra óptica sobre otros medios de transmisión.

El uso de la luz para la codificación de señales no es nuevo, los antiguos griegos usaban espejos para transmitir información, de modo rudimentario, usando luz solar. En 1792, Claude Chappe diseñó un sistema de telegrafía óptica, que mediante el uso de un código y torres y espejos distribuidos a lo largo de los 200 km que separan Lille y París, conseguía transmitir un mensaje en tan sólo 16 minutos.

La gran novedad aportada en nuestra época es la de haber conseguido “domar” la luz, de modo que sea posible que se propague dentro de un cable tendido por el hombre. El uso de la luz guiada, de modo que no expanda en todas direcciones, sino en una muy concreta y predefinida se ha conseguido mediante la fibra óptica, que podemos pensar como un conducto de vidrio -fibra de vidrio ultra delgada- protegida por un material aislante que sirve para transportar la señal lumínica de un punto a otro.

Además tiene muchas otras ventajas, como bajas pérdidas de señal, tamaño y peso reducido, inmunidad frente a emisiones electromagnéticas y de radiofrecuencia y seguridad.

Como resultado de estudios en física enfocados de la óptica, se descubrió un nuevo modo de empleo para la luz llamado rayo láser. Este último es usado con mayor vigor en el área de las telecomunicaciones, debido a lo factible que es enviar mensajes con altas velocidades y con una amplia cobertura. Sin embargo, no existía un conducto para hacer viajar los fotones originados por el láser.

La posibilidad de controlar un rayo de luz, dirigiéndolo en una trayectoria recta, se conoce desde hace mucho tiempo. En 1820, Augustin-Jean Fresnel ya conocía las ecuaciones por las que rige la captura de la luz dentro de una placa de cristal lisa. Su ampliación a lo que entonces se conocía como cables de vidrio fue obra de D. Hondros y Peter Debye en 1910.

El confinamiento de la luz por refracción, el principio de que posibilita la fibra óptica, fue demostrado por Daniel Colladon y Jacques Babinet en París en los comienzos de la década de 1840. El físico irlandés John Tyndall descubrió que la luz podía viajar dentro de un material (agua), curvándose por reflexión interna, y en 1870 presentó sus estudios ante los miembros de la Real Sociedad.¹ A partir de este principio se llevaron a cabo una serie de estudios, en los que demostraron el potencial del cristal como medio eficaz de transmisión a larga distancia. Además, se desarrollaron una serie de aplicaciones basadas en dicho principio para iluminar corrientes de agua en fuentes públicas. Más tarde, J. L. Baird registró patentes que describían la utilización de bastones sólidos de vidrio en la transmisión de luz, para su empleo en un primitivo sistema de televisión de colores. El gran problema, sin embargo, era que las técnicas y los materiales usados no permitían la transmisión de la luz con buen rendimiento. Las pérdidas eran grandes y no había dispositivos de acoplamiento óptico.

Problema 4.2

Problema 4.1

EXPOSICIÓN FIBRA ÓPTICA TEMAS 4.0 - 4.12

4.0 Fibra óptica.
4.1 Naturaleza de la luz.
4.2 Leyes de la óptica y definiciones.
4.3 Tipos de fibras.
      Fibra monomodo, índice escalonado.
      Fibra multimodo, índice escalonado.
      Fibra multimodo, índice gradual.
4.4 Estructuras de las fibras ópticas, índice escalonado.
4.5 Representación ondulatoria del rayo óptico.
4.6 Modos de propagación en guías de onda circulares.
4.7 Ecuaciones de la guía de onda dieléctrica.
4.8 Ecuaciones de onda en fibras ópticas, índice
      escalonado.
4.9 Modos de propagación en guías de onda dieléctricas.
4.10Modos de propagación en fibras ópticas, índice
      escalonado.
4.11Flujo de potencia en fibras ópticas de índice
      escalonado.
4.12Cada unidad considera ejemplos y problemas.

Fibra c3b3pticapresentacion8

View more presentations from odcatastrophe.

Un video complementario de Fibra Óptica

EXPOSICIÓN: CINTA Y MICROCINTAS, TEMAS 3.0-3.50

3.0 Líneas de Cinta y Microcintas. Definiciones.
3.1 Definiciones y características principales.
3.2 Impedancia característica. Constante dieléctrica.
3.3 Constante de propagación, atenuación y fase.
3.4 Aplicación como elemento de circuito. Parámetros
      distribuidos.
3.5 Consideraciones de diseño, en el cálculo de redes de
      acoplamiento.

Microcita

View more presentations from odcatastrophe.

EXPOSICIÓN GUIAS DE ONDA TEMAS 2.0 - 2.5

2.0 Guías de onda rectangulares y circulares.
2.1 Modos de propagación en las guías de onda
      rectangular y cilíndrica.
2.2 Ecuaciones que definen el comportamiento de las
      Guías de Onda.  
2.3 Parámetros de propagación.
      Atenuación, constante de fase,  frecuencia de corte,
      longitud de onda,  longitud de onda de corte,
      impedancia de onda, velocidad de grupo, velocidad
      de fase, pérdidas en la guía.
      Consideraciones de Diseño.
2.4 Formas de alimentación o excitación.
2.5 Aplicaciones.

Guias de onda rectangulares y circulares

View more presentations from odcatastrophe.

Examén Primer Parcial.

1.-Tipos de líneas de transmisión.

Líneas de transmisión de conductor paralelo.

Líneas de transmisión coaxial o concéntrica.

2.-¿Qué es histéresis?

Es la tendencia de un material a conservar una de sus propiedades, en ausencia del estímulo que la ha generado. Podemos encontrar diferentes manifestaciones de este fenómeno. Por extensión se aplica a fenómenos que no dependen sólo de las circunstancias actuales, sino también de cómo se ha llegado a esas circunstancias.

3.- Impedancia característica y de que parámetros  depende.

Z₀ = √ R + jLω / G + jCω

Z₀ = Impedancia característica en ohmios.
R = Resistencia de la línea en ohmios.
C = Capacitancia de la línea en faradios.
L = Inductancia de la línea en henrios.
G = Conductancia del dieléctrico en siemens.
ω = 2πf, siendo f la frecuencia en hercios
j = Factor imaginario

4.-¿Qué es la Carta de Smith? ¿Para qué sirve? ¿Qué es lo que mide?

La carta de Smith es un tipo de nomograma, usado en ingeniería eléctrica, que muestra cómo varía la impedancia compleja de una línea de transmisión a lo largo de su longitud. Se usa frecuentemente para simplificar la adaptación de la impedancia de una línea de transmisión con su carga.

La carta de Smith es un diagrama polar especial que contiene círculos de resistencia constante, círculos de reactancia constante, círculos de relación de onda estacionaria constante y curvas radiales que representan los lugares geométricos de desfase en una línea de valor constante; se utiliza en la resolución de problemas de guías de ondas y líneas de transmisión.

5.-¿Qué es un “Stub” y para qué sirve?

Es la longitud de una línea de transmisión o guía de onda que está conectada a una sola terminal. La terminal sin conectar está en circuito abierto o cortocircuitada (en el caso de las guías de onda). Sin tomar en cuenta las pérdidas de la línea de transmisión, la impedancia de entrada del stub es puramente reactiva, ya sea capacitiva o inductiva, dependiendo de la longitud eléctrica del stub y si está en circuito abierto o cerrado. La frecuencia depende de efecto inductivo o capacitivo.

Debido a que los stubs toman propiedades reactivas en por su longitud eléctrica, se encuentran en circuitos de muy altas frecuencias o microfrecuencias donde las longitudes de línea son más fáciles de manipular. Los stubs son usados en circuitos de antenas selectoras de impedancias y filtros selectores de frecuencias.   

PROBLEMA 2.6

Se tiene una línea de transmisión sin pérdidas, con porcelana como dieléctrico (єr = 6), que trabaja a una frecuencia de 400 MHz. La longitud de la línea de transmisión es de 11 m y su impedancia característica es igual a 60 Ω. Al final de la línea se conecta una carga cuya impedancia es de 90 Ω. Encuentre el coeficiente de reflexión para voltajes en la carga y la impedancia de entrada de la línea. Calcule también la impedancia que se vería a distancias de λ/2 y λ, medidas desde el generador hacia la carga.

SOLUCIÓN.

El coeficiente de reflexión para voltajes se obtiene empleando la ec.

ρ = ZL – Zo / ZL + Zo = 90 – 60 / 90 + 60 = 0.2 = 0.2 / 0°

Para calcular la impedancia de entrada se empleará la ecuación con l = 11 m y α = 0 :

Zi = Zo (1 + ρexp(-2γl) / 1 - ρexp(-2γl)) = 60 (1 + 0.2exp(-j22β) / 1 – 0.2exp(-j22β))   

Antes de realizar la operación final es preciso calcular β :

v = c /√єr = ω /β

Despejando a β y sustituyendo valores:

β = 2π x 4 x 10⁸ √6 / 3 x 10⁸ = 20.52 rad/m

Y sustituyendo ahora el valor de β en la expresión para Zi:

Zi = 60 (1 + 0.2exp(-j451.44) / 1 – 0.2exp(-j451.44)) = 71.36 + 24.17 = 75.34/ 0.32°

Para poder calcular la impedancia vista en z = -l + λ/2 y z = -l + λ, y si se desea conocer cada posición en metros, es necesario obtener primero el valor de λ:

λ = λo  / √єr = 1 m / √6 = 0.408 m

Dónde λo es la longitud de onda en el espacio libre a la misma frecuencia de 400 MHz.

De las ecuaciones se tiene que:

Z(z) = Zo (exp(-γz) + ρexp(γz) / exp(-γz) - ρexp(γz)) = Zo (1 + ρexp(2γz) / 1 - ρexp(2γz))

Por lo tanto, sustituyendo los valores especificados de z:

Z |z = -l +λ/2 = 60 (1 + 0.2exp(j2β(-11 + 0.204)) /1 - 0.2exp(j2β(-11 + 0.204)))

        = 60 (1 + 0.2exp(-j443.06) /1 - 0.2exp(-j443.06)) = 40.05 +j1.59 = 40.08/ 0.03° ohms

Z |z = -l +λ = 60 (1 + 0.2exp(j2β(-11 + 0.408)) /1 - 0.2exp(j2β(-11 + 0.408)))

        = 60 (1 + 0.2exp(-j434.69) /1 - 0.2exp(-j434.69)) = 65.54 -j24.99 = 70.15/- 0.36° ohms

TIPOS DE CABLE COAXIAL

Un cable coaxial está compuesto por dos conductores cilíndricos, generalmente de cobre, dispuestos de forma concéntrica.

El núcleo central (alma) es sólido y está separado del conductor externo (trenza metálica o malla) por un aislante.Todo el conjunto está cubierto a su vez por una gruesa capa protectora e incluso, a veces, por otro conductor que actúa de pantalla de protección frente a interferencias. 
Con esta estructura, el cable coaxial resulta ser un excelente transmisor de señales de alta frecuencia, con mínimas pérdidas por radiación y muy poco sensible a las interferencias externas.

Fundamentalmente, existen dos categorías de cables coaxiales :

Para transmisión en banda ancha.
Con una impedancia característica de 75 ohmios.Utilizado en transmisión de señales de televisión por cable (CATV, "Cable Televisión").

Para transmisión en banda base.
Con una impedancia característica de 50 ohmios. Utilizado en LAN´s. Dentro de esta categoría, se emplean dos tipos de cable: coaxial grueso ("thick") y coaxial fino ("thin").

Coaxial grueso ( "thick" ): 
Es el cable más utilizado en LAN´s en un principio y que aún hoy sigue usándose en determinadas circunstancias (alto grado de interferencias, distancias largas, etc.). 
Los diámetros de su alma/malla son 2,6/9,5 mm. Y el del total del cable de 0,4 pulgadas (aprox. 1 cm.). Como conector se emplea un transceptor ("transceiver") relativamente complejo, ya que su inserción en el cable implica una perforación hasta su núcleo (derivación del cable coaxial mediante un elemento tipo "vampiro" o "grifo").

Coaxial fino ( "thin" ): 
Surgió como alternativa al cable anterior, al ser más barato,flexible y fácil de instalar.

Los diámetros de su alma/malla son 1,2/4,4 mm, y el del cable sólo de 0,25 pulgadas (algo más de 0,5 cm.). Sin embargo, sus propiedades de transmisión (perdidas en empalmes y conexiones, distancia máxima de enlace, protección gerente a interferencias, etc.) son sensiblemente peores que las del coaxial grueso.

Con este coaxial fino se utilizan conectores BNC ("British National Connector") sencillos y de alta calidad Ofrecen más seguridad que los de tipo "grifo", pero requieren un conocimiento previo de los puntos de conexión.

Hasta hace poco, era el medio de transmisión más común en las redes locales. El cable coaxial consiste en dos conductores concéntricos, separados por un dieléctrico y protegido del exterior por un aislante (similar al de las antenas de TV).

Existen distintos tipos de cable coaxial, según las redes o las necesidades de mayor protección o distancia. Este tipo de cable sólo lo utilizan las redes EtherNet.

Existen dos tipos de cable coaxial:

Cable Thick o cable grueso: es más voluminoso, caro y difícil de instalar, pero permite conectar un mayor número de nodos y alcanzar mayores distancias.

Cable Thin o cable fino, también conocido como cheapernet por ser más económico y fácil de instalar. Sólo se utiliza para redes con un número reducido de nodos.

Ambos tipos de cable pueden ser usados simultáneamente en una red. La velocidad de transmisión de la señal por ambos es de 10 Mb.

Ventajas del cable coaxial:

La protección de las señales contra interferencias eléctricas debida a otros equipos, fotocopiadoras, motores, luces fluorescentes, etc.

Puede cubrir distancias relativamente grandes, entre 185 y 1500 metros dependiendo del tipo de cable usado

Expo 1.18 Carta de smith

La carta de Smith es un tipo de nomograma, usado en ingeniería eléctrica, que muestra cómo varía la impedancia compleja de una línea de transmisión a lo largo de su longitud. Se usa frecuentemente para simplificar la adaptación de la impedancia de una línea de transmisión con su carga.

La carta de Smith es un diagrama polar especial que contiene círculos de resistencia constante, círculos de reactancia constante, círculos de relación de onda estacionaria constante y curvas radiales que representan los lugares geométricos de desfase en una línea de valor constante; se utiliza en la resolución de problemas de guías de ondas y líneas de transmisión.

Representación de impedancias normalizadas

La intersección de un círculo r y un círculo x define un punto que representa una impedancia normalizada: r+jx. Por ejemplo, el punto P de la figura 1 representa la impedancia normalizada 0.5+j, un cortocircuito

L=-1 se representa en el punto

(-1, 0) y un circuito abierto rL=1 en el punto (1, 0).

Obtención del coeficiente de reflexión

Si pensamos en la carta de Smith como una representación en polares, la distancia de un punto al origen de coordenadas se corresponde con el módulo del coeficiente de reflexión y el ángulo con respecto al eje real positivo se corresponde con su fase:

La carta de Smith proporciona ambas escalas, tanto para la lectura del módulo (en la parte inferior) como para la lectura de la fase (sobre el círculo

r=1).

Todas las impedancias que presenten el mismo módulo del coeficiente

de reflexión se situarán sobre un círculo centrado en el origen. 

Obtención de la ROE

La expresión que relaciona la ROE con el coeficiente de reflexión:

y la comparamos con la ecuación (2) vemos que la ROE coincide con el valor de

la impedancia normalizada cuando la fase del coeficiente de reflexión es cero.

Situación de los puntos Vmax y Vmin

Partiendo de la expresión de la onda de tensión en la línea en función del coeficiente de reflexión:

es fácil comprobar que los máximos se producirán cuando la fase del coeficiente de reflexión sea cero y los mínimos cuando dicha fase sea Pi.

Transformación de impedancias

Si nos desplazamos desde la carga hacia el generador, el coeficiente de reflexión en cualquier punto z de la línea viene dado, en función del coeficiente de reflexión en la carga, por la expresión:

Un caso particular es el de las líneas sin pérdidas, donde la ecuación (10)

se reduce a:

Por lo tanto, en una línea sin pérdidas, un desplazamiento z se traduce en un cambio de fase del coeficiente de reflexión, pero el módulo se mantiene constante.

Obtención de admitancias

Partiendo de la ecuación de la impedancia vista desde un punto z hacia

la carga ZL, en una línea sin pérdidas:

obtenemos la admitancia de carga normalizada. Vemos pues como el transformador λ/4 actúa como un inversor de impedancias. Un desplazamiento de un cuarto de longitud de onda equivale a un cambio de fase de pi radianes en el coeficiente de reflexión, por lo tanto el punto de la admitancia está diametralmente opuesto al de la impedancia correspondiente.

También es posible emplear la carta de Smith como diagrama de admitancias, muy útil para resolver problemas de conexiones de líneas en paralelo (donde las admitancias se suman). Si se trabaja con admitancias normalizadas las posiciones de cortocircuitos y circuitos abiertos están invertidas respecto de la carta de impedancias y también se invierte la posición de los lados capacitivo e inductivo.

El resultado importante es el hecho de que el coeficiente de reflección del voltaje y la impedancia de entrada a la línea normalizada en el mismo punto de la línea, están relacionados por la carta de Smith. En la parte exterior de la carta hay varias escalas.

Precisión de la carta de SMITH

La escala angular en el borde tiene divisiones de 1/500 de una longitud de onda (0,72 grados) y la escala del coeficiente de reflexión se puede leer a una precisión de 0,02. Con lo que se demuestra que es absolutamente suficiente para la mayoría de los propósitos. Por ejemplo, si la longitud de onda en cable coaxial en 1 GHz es 20 centímetros, la carta de SMITH localiza la posición a lo largo del cable a 20/500 centímetro o 0,4 milímetros y ellas están claros a cualquier persona que ha manejado el cable en el 1GHz que no puede ser cortado a esta precisión.

Si se requiere más precisión, una sección agrandada de la carta se puede hacer fácilmente con una fotocopia.

Ventajas Principales de la CARTA de SMITH

A continuación se mencionan algunas ventajas de la carta de SMITH :

Es una representación gráfica directa, en el plano complejo, del coeficiente de reflexión complejo.

Es una superficie de Reimann, en que es cíclico en números de mitad-longitudes de onda a lo largo de la línea. Pues el patrón derecho de la onda repite cada media longitud de onda, esto es enteramente apropiado. El número de medias longitudes de onda se puede representar por el número de la bobina.

Puede ser utilizado como calculadora de la impedancia o de la entrada, simplemente dándole vuelta con 180 grados.

El interior de la región circular gamma de la unidad representa el caso pasivo de la reflexión, que es lo más a menudo posible la región del interés.

La transformación a lo largo de la línea da lugar a un cambio del ángulo, y no al módulo o al radio de gamma. Así, los diagramas se pueden hacer rápidamente y simplemente.

Muchas de las características más avanzadas de la microonda circulan, por ejemplo las regiones de la figura del ruido y de la estabilidad, mapa sobre la carta de SMITH como círculos.

El "punto en el infinito" representa el límite del aumento muy grande de la reflexión, y así que por lo tanto nunca necesite ser considerado para los circuitos prácticos.

Los mapas verdaderos del eje a la variable derecha del cociente de la onda (SWR). Una transferencia simple del lugar geométrico del diagrama al eje verdadero en el radio constante da una lectura directa del SWR.

PROBLEMA 2.5

Un generador de señales está conectado a una línea de transmisión cuya impedancia característica vale 100 Ω. La línea mide 10 metros y el dieléctrico en su interior tiene una permitividad relativa de 8.8. Al final de la línea se conecta una carga cuya impedancia de entrada vale 100 Ω. SI el generador tiene una resistencia interna de 1 Ω y un voltaje de salida en circuito abierto igual a 3cos(2π x 10⁸)t V, encuentre a)las expresiones matemáticas instantáneas para el voltaje y corriente en cualquier punto de la línea, y b)la potencia promedio que se le entrega a la carga.

SOLUCIÓN.

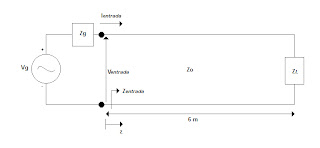
De acuerdo con los datos proporcionados, el circuito se puede representar de la siguiente forma:

Vg = 3 / 0                 f = 100 MHz

    Zg = 1 Ω               Zo = 100 Ω – ZL

Como la línea está acoplada, la impedancia que se ve en todos los puntos de la línea es la misma y, por lo tanto, la impedancia de entrada también vale eso:

                                                                     Zentrada = 100 Ω

La parte izquierda del circuito se puede representar ahora como:

De donde:

Ventr = [ Zentr / Zg + Zentr ] Vg = (100/101)(3/ 0) = 2.97 / 0 V

Ientr = (1 / Zg + Zentr)Vg =

 3 / 0 / 101 = 0.0297 / 0 A

Si se considera que la atenuación α es despreciable, entonces:

γ = jβ = jω /v = jω√εr / c = j(2πx10⁸)√8.8 /3x10⁸ = j6.2129 rad/m

Por lo tanto, se tiene que para cualquier punto de la línea a una distancia z a la derecha de las terminales de la entrada, el voltaje está dado por:

V(z) = (Ventr)exp(-jβz) = (2.97expj0)exp(-j6.2129) = 2.97exp(-j6.2129) V

Y acordemente la corriente es igual a:

I(z) =(Ientr)exp(-jβz) = 0.0297exp(-j6.2129) A

Finalmente, se obtinen las expresiones perdidas en función del tiempo, para cualquier punto de la línea:

V(z,t) = Re[V(z)exp(jωt)] = Re[2.97exp(-j6.2129) * exp(j2πft)]

V(z,t) = 2.97cos[2πx10⁸t – 6.2129] V

I(z,t) = Re[I(z)exp(jωt)] = Re[0.0297exp(-j6.2129) * exp(j2πft)]

I(z,t) = 0.0297cos[2πx10⁸t - 6.2129] A

Para el punto específico donde está la carga, las expresiones instantáneas se obtienen sustituyendo z = 10 m  en las ecuaciones anteriores.

Por lo que se refiere a la potencia promedio entregada a la carga, está debe ser igual a la potencia promedio de entrada, ya que está considerando que la línea no tiene pérdidas (α=0). De allí que, a partir de los fasores de volaje y corriente:

(Pprom) = (Pprom)entr = ½ Re(V(z)I’(z))

                 = ½ Re[2.97exp(-j6.2129)* 0.0297exp(j6.2129)]

                 = ½ (2.97 x 0.0297) = 0.0441045 W.

PROBLEMA 2.4

2.4 Obtenga los valores de la impedancia característica, la constante de atenuación, la constante de fase y la velocidad de fase de la línea bifilar de oro del ejercicio 2-2. Si la línea mide 1 km ¿Cuánto tiempo tardará una señal en viajar desde el generador hasta el extremo opuesto?

F	L	C	R	G
1 kHz	1.02 μH/m	0.1062 nF/m	3.881 m Ω/m	0.4005 nano mho/m
10 kHz	0.92 μH/m	0.1062 nF/m	6.949 x 10¹³ Ω /m	4.005 nano mho/m
1 MHz	0.92 μH/m	0.1062 nF/m	6.949 x 10¹⁴ Ω /m	4.005 x 10⁻⁴ mho/m

IMPEDANCIA CARACTERÍSTICA

Z₀ = √(R + jL) / (G + jC)

Para f = 1 kHz.

Z₀ = √ 3.881x10⁻³ + j(2π)(10³)(1.02x10⁻⁶) / 0.4005x10⁻⁹ + j(2π)(10³)(0.1062x10⁻⁹)

Z₀ = 87.836 – j87.781 Ω

Para f = 10 kHz.

Z₀ = √ 6.949x10¹³ + j(2π)(10⁴)(0.92x10⁻⁶) / 4.005x10⁻⁹ + j(2π)(10⁴)(0.1062x10⁻⁹)

Z₀ = 2282629954 – j2281036934

Para f = 1 MHz.

Z₀ = √ 6.949x10¹⁴ + j(2π)(10⁶)(0.92x10⁻⁶) / 4.005x10⁻⁴ + j(2π)(10⁶)(0.1062x10⁻⁹)

Z₀ = 2600.439 – j1471.976

CONSTANTE DE PROPAGACIÓN

γ = √(R + jwL) (G + jwC)

Para f = 1kHz

γ = √[3.881x10⁻³ + j(2π)(10³)(1.02x10⁻⁶) ][ 0.4005x10⁻⁹ + j(2π)(10³)(0.1062x10⁻⁹)]

γ = 1.921x10⁻⁵ + j6.802x10⁻⁵ 

Para f = 10kHz.

γ = √ [6.949x10¹³ + j(2π)(10⁴)(0.92x10⁻⁶) ][ 4.005x10⁻⁹ + j(2π)(10⁴)(0.1062x10⁻⁹)]

γ = 48.160 + j48.13

Para f = 1 MHz.

γ = √ [6.949x10¹⁴ + j(2π)(10⁶)(0.92x10⁻⁶) ] [4.005x10⁻⁴ + j(2π)(10⁶)(0.1062x10⁻⁹)]

γ = 63983.621 + j36217.883

α parte real de γ.

β parte real de γ.

VELOCIDAD DE PROPAGACIÓN

Vp =ω / β = 2πf / β

Para  f = 1 kHz.

Vp = 2π x 10³ / 6.802x10⁻⁵ = 92372615.51 m/s

Para  f = 10 kHz.

Vp = 2π x 10⁴ / 48.13 = 1305.4613 m/s

Para  f = 1 MHz.  

Vp = 2π x 10⁶ / 36217.883 = 173.224 m/s

ANALIZANDO RESULTADOS

Conforme la frecuencia aumenta, su componente imaginaria tiende a 0 y la parte real tiende al mismo valor que se obtendría para una línea sin perdidas al hacer R y G = 0 Z₀ = √L/C, así mismo al aumentar la f, γp tiende al valor que tendría la velocidad de propagación en un medio con εr = 8.8 (oxido de aluminio) y sin perdidas.

V = c / √εr = 101129979.4 m/s

TIEMPO DE RETARDO

Td = l /Vp

Como l = 10³ m.

f	Td
1 kHz	10.825 µs
10 kHz	766.012 ms
1 MHz	5.772 s